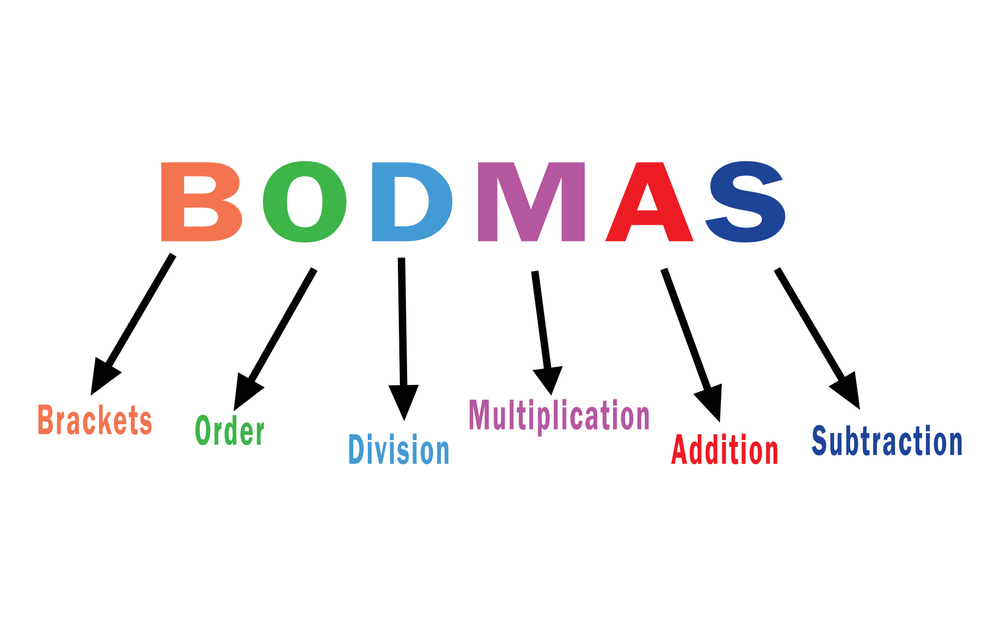
BODMAS, an acronym representing Bracket, Of, Division, Multiplication, Addition, and Subtraction, is a fundamental guideline in mathematics that establishes the sequence in which mathematical operations should be carried out when solving equations or expressions. Its purpose is to simplify and streamline the process of tackling complex mathematical problems.
- BODMAS Full Form: Understanding Brackets (B)
- BODMAS Full Form: Orders (Exponents and Roots) (O)
- BODMAS Full Form: Division (D) Operation in BODMAS
- BODMAS Full Form: Multiplication (M) with in BODMAS
- BODMAS Full Form: Addition (A) Step in BODMAS
- BODMAS Full Form: Subtraction in Context of BODMASP
- BODMAS Full Form: FAQ about BODMAS
Understanding Brackets (B)
Brackets, denoted by the ‘B’ in BODMAS, play a crucial role in mathematics. Think of them as mathematical containers that hold and isolate specific parts of an expression. Their primary purpose is to dictate the order in which certain operations should be performed, ensuring mathematical clarity and precision.
Examples of Solving Expressions Inside Brackets
Example 1: Simple Arithmetic
Consider the expression: 2 * (3 + 4)
Here, the brackets indicate that you should first solve what’s inside them. So, you calculate 3 + 4, which equals 7. Then, you multiply the result by 2:
2 * 7 = 14
So, the final answer is 14.
Orders (Exponents and Roots) (O)
Orders, denoted by the ‘O’ in BODMAS, refer to exponents and roots in mathematics. They are fundamental concepts that deal with raising numbers to powers and extracting roots, and they hold a significant place in mathematical calculations.
Exponents involve raising a number to a specific power. For example, 2^3 means multiplying 2 by itself three times (2 * 2 * 2), resulting in 8. Exponents are used to represent repeated multiplication and play a critical role in various mathematical and scientific fields.
Roots are the opposite of exponents. They help us find the “opposite” of raising a number to a power. For instance, the square root (√) of 25 is the number that, when multiplied by itself, gives 25. In this case, it’s 5 because 5 * 5 = 25. Roots are essential for solving equations, understanding proportions, and dealing with real-world measurements.
Division (D) Operation in BODMAS
Division, denoted by the ‘D’ in BODMAS, is a fundamental mathematical operation that represents the process of sharing or distributing a quantity into equal parts. It plays a vital role in various mathematical calculations and real-world problem-solving.
- In division, you have a dividend (the quantity you want to divide) and a divisor (the number by which you divide the dividend). The result of division is called the quotient.
For example, consider the expression 12 ÷ 3:
- Here, 12 is the dividend, and 3 is the divisor.
- When you divide 12 by 3, you are essentially asking how many times 3 can fit into 12 evenly.
- The answer is 4 because 3 can fit into 12 four times without any remainder.
Multiplication (M) with in BODMAS
- Multiplication, represented by the ‘M’ in BODMAS, is a fundamental mathematical operation that involves combining or repeated addition of numbers. It plays a crucial role in mathematical calculations and is essential for solving various types of problems.
- At its core, multiplication is the process of finding the total when you add a number to itself multiple times.
For example, 3 multiplied by 4 (3 × 4) means adding 3 to itself four times: 3 + 3 + 3 + 3, which equals 12.
Addition (A) Step in BODMAS
The addition step in BODMAS, represented by the ‘A,’ is the mathematical operation of combining numbers to find their total or sum. It’s one of the basic arithmetic operations and plays a crucial role in various mathematical calculations. Here’s a breakdown of the addition step within BODMAS:
- Addition involves taking two or more numbers and finding their combined total. For example, when you add 3 and 4, you get 7 (3 + 4).
- For example, in the expression 2 + 3 × 4, you first perform the multiplication (3 × 4 = 12) and then add 2 to the result, yielding 14.
Subtraction in Context of BODMAS
Subtraction, indicated by the ‘S’ in BODMAS, is a fundamental mathematical operation that involves finding the difference between two numbers or quantities. It plays a significant role in mathematical calculations, especially when applied within the context of BODMAS (Brackets, Orders, Division, Multiplication, Addition, Subtraction). Here’s a closer look at subtraction within BODMAS:
- In BODMAS, subtraction takes place after multiplication and division but before addition. This means that when you encounter an expression that combines multiple operations, you perform subtraction only after addressing any multiplication or division.
- For instance, in the expression 5 + 6 – 2 × 3, you first execute the multiplication (2 × 3 = 6), then perform addition (5 + 6 = 11), and finally carry out the subtraction (11 – 6 = 5).
Practical Examples and Exercises
Solve this expression using BODMAS: (10 – 2) × 5 ÷ 3 + 4^2
Solution:
- Start with the innermost brackets: 10 – 2 = 8
- Then, perform the exponent: 4^2 = 16
- Next, multiply 5 by 8: 8 × 5 = 40
- Finally, divide by 3 and add the result: 40 ÷ 3 + 16 = 13.33 + 16 = 29.33
FAQs About BODMAS
BODMAS stands for Brackets, Orders (Exponents and Roots), Division, Multiplication, Addition, and Subtraction. It is an acronym used to remember the order in which mathematical operations should be performed in expressions.
BODMAS is important because it provides a standardized way to evaluate mathematical expressions, ensuring that calculations are carried out consistently. Without BODMAS, different people might interpret expressions differently, leading to confusion and incorrect results.
Common mistakes include forgetting to apply the order of operations correctly, neglecting brackets, and not working from left to right within each operation (e.g., multiplying before dividing).
No, the BODMAS order of operations is a fundamental rule in mathematics and applies universally to all mathematical expressions. There are no exceptions.
