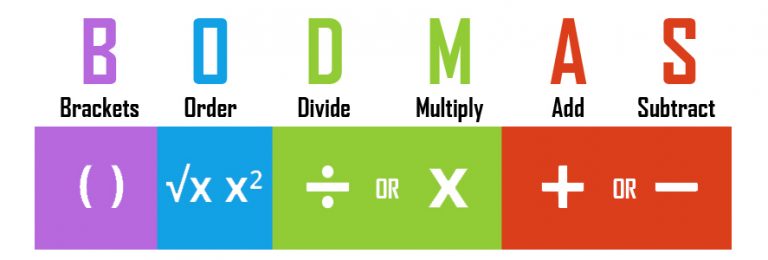
The term BODMAS rule might help you recall which operations to perform in which sequence while working out math problems. An arithmetic phrase needing several operations, such as addition, subtraction, multiplication, and division is challenging to solve when compared to operations involving two numbers. A two-number operation is easy to perform, but how can you simplify a bracket and solve an expression containing brackets and multiple operations? In this situation, the BODMAS rule is intended to resolve difficult arithmetic operations. O represents for the order of powers or roots, D for division, M for multiplication, A for addition, and S for subtraction. B stands for brackets.
What is the BODMAS Rule?
You can apply the BODMAS rule to solve any arithmetic statement, which entails first resolving terms enclosed in brackets, then simplifying exponential terms before moving on to division and multiplication operations, and ultimately focusing on addition and subtraction. The correct solution is always obtained by using the BODMAS rule in the proper order.
The terms in the brackets can be summarised quickly. Thus, we can carry out the operations of division, multiplication, addition, and subtraction in the sequence indicated by the brackets. Numerous brackets in an expression can be solved simultaneously if they are of the same type.
Order of Operations
For the purpose of evaluating a particular numerical statement in logic-focused subjects like mathematics, the order of operations is a set of general principles that serve as standards. The result can be calculated easily using a straightforward summation that only requires two numbers and a single operation, or sign. The four operations are addition, subtraction, multiplication, and division
Interpretation of BODMAS Rule
The this Rule demonstrates which operations to carry out when solving an expression and in what sequence. The this rule states that when an expression has brackets ((),, []), we must first solve or simplify the bracket before moving on to the other operations. These operations are division, multiplication, addition, subtraction, and ‘order’, which refers to powers and roots, etc. You’ll get the incorrect solution if you approach the problem in the incorrect manner.
The BODMAS rule can be applied if the expression has several operators. In this case, the words inside the bracket [()], from the innermost to the outermost bracket, as well as any roots or exponents, must first be simplified. then perform division or multiplication operations going from left to right. To reach the right answer, utilize addition or subtraction last. The “O” in the BODMAS full form also stands for “Order,” which refers to numbers with powers, square roots, and other special types of numbers. This must be kept in mind.
Full-Form of BODMAS
Brackets, Orders, Division, Multiplication, Addition, and Subtraction are collectively referred to as BODMAS. When using the BODMAS rule, these steps should be completed in the correct order.
| B | Bracket | (), {}. [] |
| O | Order of | Powers & Exponents, Indices, Square roots |
| D | Division | \ |
| M | Multiplication | * |
| A | Addition | + |
| S | Subtraction | – |
For the purpose of producing reliable results, it is necessary to adhere to the rule that demonstrates how to solve an equation in the proper sequence (order of precedence).
BODMAS Rule VS PEMDAS Rule
| BODMAS | Operators | PEMDAS |
| Bracket | (), {}. [] | Parenthesis |
| Order | √ or x2 | Exponents |
| Division | / or * | Multiplication |
| Multiplication | * or / | Division |
| Addition | + | Addition |
| Subtraction | – | Subtraction |
When to use the BODMAS Rule?
BODMAS is used when a mathematical equation includes many operations. There are a number of guidelines that must be adhered to in the correct order while using the BODMAS technique. This gives each mathematical expression the proper structure to produce a distinct solution.
Rules & Conditions
- If any brackets exist, open them and then add or remove the terms. For instance, a + (b + c) = a + b + c, a + (b – c) = a + b – c
- If a negative sign appears, simply open the bracket and multiply the negative sign with each phrase inside. For instance, a – (b + c) ⇒ a – b – c
- If there is a term just outside the bracket, multiply it by each term inside. For example, a(b + c) ⇒ ab + ac
Easiest Method to Remember BODMAS Rule
The BODMAS rule can be remembered by keeping in mind the following simple principles:
Step 1: Simplify the brackets first.
Step 2: Make a list of all the exponential terms and solve them in step two.
Step 3: Multiply or divide the integers (left to right)
Step 4: Complete the addition or subtraction (left to right)
Common Mistakes while applying BODMAS Rule
There are a few common errors that can be made while utilizing the BODMAS rule to simplify expressions, which are given below:
- We could be confused by multiple brackets and end up with the wrong answer as a result. Numerous brackets in an expression can be solved simultaneously if they are of the same type.
- It’s incorrect to assume that addition comes before subtraction and that multiplication comes before division. When choosing these procedures, remembering the left-to-right rule will help you get the right answer.
- Addition and subtraction are same-level operations that must be completed after multiplication and division. Multiplication and division are same-level operations that must be completed in the sequence of left to right (whichever appears first in the statement). Since D comes before M in BODMAS, if you solve division first and then multiplication (which is on the left side of division), you can receive the wrong answer.
- In some cases, a mistake is made as a result of an inability to understand integer addition and subtraction. For instance, 1 – 3 + 4 equals – 2 + 4 = 2. However, there are instances in which the following mistakes are made and the incorrect answer is given, such as when 1- 3 + 4 = 1 – 7 = – 6.
Things to Remember
- BODMAS stands for brackets, order, division, multiplication, addition, and subtraction. This rule demonstrates how to solve an equation based on the precedence (order of operations).
- The order of operations is a set of common principles that establishes guidelines for which process to execute first to examine a given numerical statement in logic-oriented courses like mathematics.
- BODMAS is used when a mathematical equation includes many operations. This gives each mathematical expression the proper structure to produce a distinct solution.
- The BODMAS rule states that we must first solve or simplify the brackets before moving on to the of (powers and roots, etc.), of, division, multiplication, addition, subtraction, and subtraction from left to right in a given mathematical expression that contains the following signs: brackets, multiplication, of, addition, subtraction, and division.
- Mathematicians can solve a mathematical expression using the BODMAS rule. BODMAS is a crucial concept that has shown to work well in numerous circumstances demanding rapid computations.
Sample Questions
According to BODMAS, we perform multiplication before addition. So, 3 x 2 = 6, and 5 + 6 = 11.
Following BODMAS, we perform multiplication first: 2 x 4 = 8. Then, we perform subtraction and addition: 8 – 8 + 3 = 3.
Using BODMAS, we simplify the expression inside the brackets first: 4 + 2 = 6. Then, we perform division and subtraction: 12 ÷ 6 – 1 = 2 – 1 = 1.
Following BODMAS, we simplify the expression inside the brackets first: 2 – 1 = 1. Then, we perform multiplication and division: 4 x 1 ÷ 5 = 4 ÷ 5 = 0.8. Finally, we perform addition: 3 + 0.8 = 3.8.
Using BODMAS, we perform multiplication first: 3 x 4 = 12. Then, we perform division: 6 ÷ 2 = 3. Finally, we perform addition and subtraction: 2 + 12 – 3 = 11.
Following BODMAS, we simplify the expression inside the brackets first: 4 – 3 = 1. Then, we perform multiplication: 2 x 1 = 2. Next, we perform addition and subtraction: 10 – 2 + 5 = 13.